摘 要： 為了更好地補償功率放大器的非線性，提出一種新型多步迭代算法來求取數字預失真器。新算法結合了多步迭代算法與頻域削峰技術，使功放在保證工作效率的同時更大程度提高其線性度。實驗結果顯示，該方法較傳統的線性化技術有明顯優勢，功放輸出信號的ACPR可改善20.66 dB。

關鍵詞： 功率放大器；迭代；數字預失真；削峰

0 引言

在現代通信系統中，由于頻帶資源越來越緊張，頻譜的利用率越來越受到重視。為解決該問題，多種高頻譜利用率的傳輸技術和調制方式被相繼提出，但是這類技術所傳輸的信號通常具有較高的峰均比和較寬的頻帶[1]。因功率放大器本身存在非線性特性，寬帶信號經其放大后會產生失真，所以現代通信系統中對功放的線性度有了更高的要求。

目前，提高功率放大器線性度的主要方法有前饋線性化技術、負反饋技術、包絡消除和恢復技術、LINC技術及數字預失真技術等。其中數字預失真技術因不存在穩定性問題且適用的帶寬較寬、精度高、成本低等特點受到了廣泛的關注。

數字預失真的基本原理如圖1所示，即在功率放大器的前端級聯一個特性與之相反的數字預失真器DPD，從而使整個系統呈線性效果。

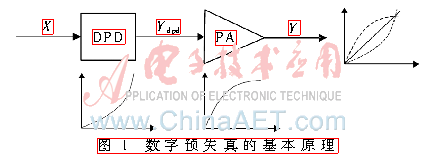
數字預失真的基本原理也可以理解為：在數字預失真技術中，首先對待優化功率放大器（PA）建立行為模型，然后通過模型求逆[2]的方法得到對應數字預失真器（DPD）。將該數字預失真器級聯到功放的前端，如圖1所示，則可達到提高該功率放大器線性度的目的。

為使上述所求數字預失真器能夠更好地補償功放的非線性，且保證功率放大器的工作效率，一種新型迭代算法被提出。

1 記憶多項式模型（MP）

記憶多項式模型是目前較為流行的一電腦電感器種模型，其在對有記憶效應的功放進行預失真處理時有很好的性能，且模型的復雜度較低，便于實現。所以本文基于該模型對功率放大器進行數字預失真處理。

記憶多項式的數學表達式通常為：

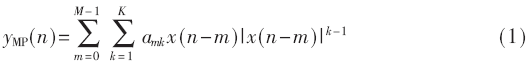
其中，amk為模型的系數，K為模型的階次數，M為模型的記憶深度。由于多項式中的階次數K、記憶深度M影響著模型的精確度，所以選取合適的模型階次數及記憶深度也很重要。實際應用通過比較不同K、M情況下模型輸出與實際輸出的歸一化均方誤差（NMSE）來確定最佳的模型階次數及記憶深度值[3]，如此確定了功放最終行為模型的數學表達式。

記憶多項式表達式（1）可以等價為：

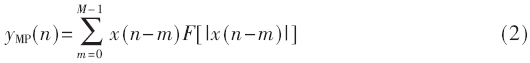
在基于記憶多項式模型的數字預失真方法中，無論是功率放大器的模型還是預失真器的模型，均可等價為存在M個查找表，且每個查找表的深度為建模信號的點數。由式（2）可看出，該查找表的具體內容與輸入信號的幅度直接相關。所以研究功放輸入信號的時域特性是十分有意義的，下面將通過MATLAB對功放輸入信號的時域特性進行分析。

2 功放輸入信號的時域特征

由功率放大器的AM-AM特性曲線知，功放的非線性失真表現為對輸入信號的峰值壓縮。為使整個放大系統輸出呈線性，所以希望功放的輸入信號的峰值預先有相應擴張的特性，即功放輸入信號較原信號有較高的峰均比（PAPR）。圖2為原信號及預失真信號的時域波形。

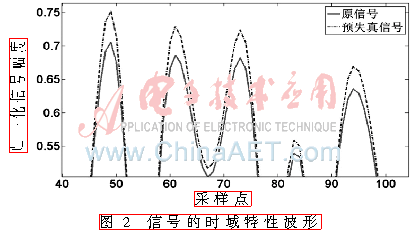
由圖2可見，預失真信號在幅值較大的區域內有信號擴張的特性。即在數字預失真技術中，通過對功放模型求逆方法得到的數字預失真器DPD對信號峰值有擴張作用[4]，該預失真器初步實現了對功放非線性的補償。

通過MATLAB求解得各信號的峰均比(PAPR)如表1所示。

由表1可看出，信號經過功率放大器后，其PAPR降低，而經過預失真器后PAPR反而提高。如此，當輸入信號經過DPD后，信號失真表現為峰值擴張，其PAPR增加；而當該信號經過功放 大功率電感廠家 |大電流電感工廠